Chapter Two
Do Things Look Flat?
When we set before our Eyes a round Globe, of any uniform color, v.g. Gold, Alabaster, or Jet, ’tis certain, that the Idea thereby imprinted in our Mind, is of a flat Circle variously shadow’d, with several degrees of Light and Brightness coming to our Eyes.
– John Locke, An Essay Concerning Human Understanding (1690/1975, p. 145, italics suppressed)
i.
I’ve put a penny on my desk, and I’m viewing it obliquely. Does it look circular? Or, instead, do I only know or judge that the penny is circular, while the figure it presents to my sight – its actual visual appearance – is an ellipse? I gaze out my window and see a row of streetlights. Does it look like they shrink as they recede into the distance? Or do they all look the same size? Get out a penny, open the blinds, try it yourself. (I’ll wait.) What do you think?
A long line of philosophers, stretching at least from Malebranche (1674/1997)[1] though David Armstrong (1955), Roderick Chisholm (1957), and John Austin (1962), to Michael Tye (2000), Alva Noë (2004), and Sean Kelly (2008), has said the following: There’s a sense in which the obliquely viewed penny looks elliptical and the distant streetlights look smaller, and a sense in which they don’t. Tye says that the coin looks like an object that is really round and also that the coin looks “elliptical from here”. He says the streetlights look the same “objective size” but also that the nearer ones look “larger from here”. Noë uses similar terminology and furthermore emphasizes that it’s just what it is for a coin to look circular that it present varying elliptical appearances depending on the angle of view. According to Noë, our visual experience always has, simultaneously, two “aspects” – a perspectival aspect (corresponding to the coin’s elliptical appearance) and an aspect reflecting our experience of the constancy of the objects we see (corresponding to our experience of the coin as genuinely circular, regardless of viewing angle). Kelly argues, contra Noë, that we don’t experience the circularity and ellipticality simultaneously but rather flip between the different ways of experiencing the coin, much as we flip, in a “Gestalt shift”, between different ways of seeing an ambiguous figure like a Necker cube or Wittgenstein’s duck-rabbit – with circularity being the primary and ordinary experience. All agree with the apparently commonsensical view that the penny both looks circular, in one sense, and also has an elliptical “apparent shape” that we at least sometimes experience.
The view is attractive. Maybe you feel tugged both ways by the questions in the opening paragraph, as I do. A dual aspect view – whether simultaneous like Tye’s and Noë’s or like Kelly’s involving a shift from one way of seeing to the other – embraces both sides of the ambivalence. You get your ellipse and your circle too. Still, not every philosopher is on board. John Locke (1690/1975), for example, seems to embrace a just-the-ellipse view, as does C.D. Broad (1925).[2] On the other side, A.J. Ayer (1940) and Charles Siewert (2006) say they see only the circle and that there is no elliptical aspect to their experience whatsoever. [3] Now maybe Locke, Broad, Ayer, and Siewert are just wrong. Indeed, some of them must be – assuming that they’re speaking the same language, not just talking at cross-purposes, and that despite their disagreement they have more or less the same type of visual experience. Such disagreements, as well as disagreements within the dual aspect camp, seem to betray a difficulty in the introspective task. So who is right? (There is a fact about who, if anyone, is right in this matter, isn’t there?)
ii.
Philosophers at least since Descartes have tended to embrace the view that nothing is so obvious, so immune to doubt, so easy to know, as one’s own ongoing conscious experience. Descartes says, or seems to say (in his second Meditation, 1641/1984), that although it’s possible to doubt anything at all about the outside world (since you might be dreaming or deceived by a demon) it’s not possible to doubt what your sensory experiences are, which seem to be produced by that outside world. Similarly, H.H. Price writes:
When I see a tomato there is much that I can doubt. I can doubt whether it is a tomato that I am seeing, and not a cleverly painted piece of wax. I can doubt whether there is any material thing there at all. Perhaps what I took for a tomato was really a reflection; perhaps I am even the victim of some hallucination. One thing however I cannot doubt: that there exists a red patch of a round and somewhat bulgy shape, standing out from a background of other colour-patches, and having a certain visual depth, and this whole field of colour is directly present to my consciousness (1932, p. 3).
Although one may doubt anything at all about the external world, the basic facts about one’s own current sensory experience are immediately obvious, unchallengeable, beyond all doubt – including, according to Price, the experience of depth and shape in a tomato, or for that matter a penny (p. 55-56, 207).
I don’t share their confidence. What exactly is my sensory experience as I stare at a penny? My first and recurring inclination is to say that the penny looks just plain circular, in a three-dimensional space – not elliptical at all, in any sense or by any effort I can muster. However, I also find that if I dip my head lower to view the penny from flatter angle, I begin to see how one might think it looks elliptical. Closing one eye helps too. I open my eye again, sit up straight, and find myself confused. Am I still experiencing the ellipse? Maybe not. But neither can I say I noticed any Gestalt shift. The lampposts puzzle me, too, in a somewhat different way – for in that case I feel more pulled toward the idea that they look like they shrink into the distance. How could the penny seem to me so convincingly nothing-but-circular most of the time, while the lampposts seem to shrink? If there’s perspectival distortion in the one case, why not in the other? Could it be that my visual experience is just disorganized, so that there’s no simple relationship between viewing angle and apparent shape, between viewing distance and apparent size?
Maybe my terms and concepts are muddled. What is it for something to “look elliptical”? Is my confusion, and the philosophical dispute – the dispute between Locke and Siewert, between them and Noë, between Kelly and pretty much everyone else – entirely linguistic, or purely theoretical, while the visual experience itself is utterly obvious?
Or am I simply a poor introspector? Maybe the fact that my own phenomenology in this case doesn’t seem obvious to me reveals my introspective ineptitude. I mean that remark not at all ironically or disingenuously. And yet I’m not sure I should trust other philosophers’ introspections either. Nor am I hopeful (as Kelly is, for example) that psychological experimentation will soon yield cleanly interpretable results in matters of this sort.
I wish I could find my way through this morass. I can’t. So I am to drag you down into it with me.
iii.
There are several ways to transform a circle into an ellipse, but the most natural in this context is to project it obliquely onto a two-dimensional plane – presumably a plane perpendicular to the line of sight. Let’s suppose that’s how the geometrical transformation is supposed to proceed in the case of the coin: The coin “looks elliptical” or has an elliptical “apparent shape” because projecting it along the line of sight onto a plane perpendicular to that line produces an elliptical figure. Plausible enough?
It’s tempting, then, to generalize: The apparent shape of any normal object is determined by its two-dimensional projection onto a plane perpendicular to the line of sight. It’s the shape that would perfectly occlude the object if pasted onto a flat interposing screen, the figure it would leave in a photograph. (In conversation I sometimes hear, as though it obviously settled the matter: Well, of course the penny looks elliptical. If you took a photo, that’s the shape you’d see on the print.) Most of the philosophers I’ve discussed appear to either invite or explicitly embrace the idea that perspectival shape is the same as shape projected on an intervening plane. Tye, for example, writes that the coin looks “elliptical from here” because “it has a shape that would be occluded by an ellipse placed in a plane perpendicular to the line of sight” (2000, p. 79). Noë writes that “perspectival size” and “perspectival shape” correspond to the “patch one must fill in on a plane perpendicular to the line of sight in order to perfectly occlude the object from view” (2004, p. 81-82).
Price is an interesting exception. Price claims that the degree of perspectival distortion varies with distance – that we experience nearby objects in their true shapes and sizes (hence the “bulgy” red patch when examining a tomato), while more distant objects look progressively flatter and more distorted. An obliquely viewed penny at arm’s length might, then, look circular, while a coliseum viewed at the same angle from a mountain looks elliptical. A matchbox on one’s desk looks fully three-dimensional; a tower seen across the quad appears partly flattened out, though not entirely flat; the mountains in the distance look almost as though painted on a wall. (At least this seems to be Price’s picture in 1932, p. 218-221. Elsewhere [e.g., p. 207] Price seems to accept that the obliquely viewed penny does look elliptical. I’m afraid I don’t see how all his remarks can be made fully consistent.) In certain moods I do find myself tempted by Price’s idea that nearby things appear in all their three-dimensional glory while the far distance is a painted backdrop. But how about the middle distance? If the tower’s square corner doesn’t look ninety degrees but also doesn’t look entirely flat, how does it look? A hundred and thirty-five degrees? Only with an extra burst of sympathy and the prop of the theoretical appeal of a gradual progression toward flatness, can I find any attraction to that view.
If we accept, contra Price, but apparently with Locke, Tye, Noë, and others, that the perspectival apparent shape of objects is defined by the projection they would make on a plane perpendicular to the line of sight, then it follows that my hat viewed from the top also looks circular or elliptical, that the orange before me looks circular, that the obliquely viewed book on my desk appears (roughly) hexagonal – and, in short, that everything looks or appears (in the relevant perspectival sense of “looks” or “appears”) two-dimensional, flat. The peculiarity of this view can be missed when the object in question, like a penny, is already something approximately flat.
I don’t know whether most of the philosophers who claim that the coin, in some sense, presents an elliptical “apparent shape” would also accept the view that everything (in that same sense) looks flat; I suspect some would not. Yet it isn’t evident where exactly to put on the brakes. Can something’s apparent shape be defined by its two-dimensional projection without its presenting any sort of flat appearance? (It is, perhaps, neither flat nor non-flat, because depth is simply unrepresented? – but then the word “elliptical”, with its planar character, is misleading; it would be better to say simply that it has a certain angular extent, as in Reid 1764/1997, IV.9[4].)
The geometry of planar projection defies intuitive phenomenology. To account for the streetlights smalling off into the distance, we can have the projecting lines converge upon the eye, rendering more distant objects smaller in the projective plane – no problem there; that seems natural enough. But a peculiar result follows from the fact that lines coming from the side will intersect the plane obliquely: The planar projections of objects off the central line of sight will be considerably larger than their straight-ahead counterparts – weirdly larger, if projective size is supposed to be isomorphic to apparent size. They’ll be stretched especially in the direction of deviation from the center (see Figure 2.1). Note the considerably larger shadow the right figure casts in the plane. The rays crossing the plane obliquely spread over a larger area. For the same reason, winter is colder than summer. Also for this reason, traditional cameras cannot accurately capture panoramic views. But objects off the central line of sight don’t actually look substantially larger and horizontally stretched, do they? It’s certainly not a position I recall any philosopher or psychologist espousing in print. Yet it appears to follow straightforwardly from defining apparent size and shape by the geometry of planar projection.
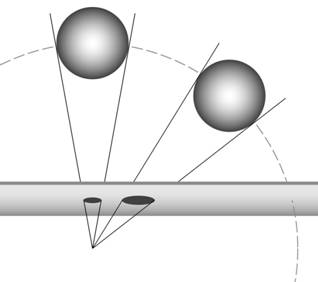
Figure 2.1[*]
A natural way to avoid this result would be to project objects not onto a plane but rather onto a sphere centered at the eye. (Imagine bending the plane back on both sides until it forms a sphere centered around the convergence point.) Using spherical rather than planar projection would also capture the idea, which one sometimes hears (in Tye 2000, p. 78 for example), that apparent size is proportional to visual angle subtended. But now we’ve lost our ellipse. The projection of a circular region onto a spherical surface isn’t elliptical: The ellipse is a planar figure. The resulting projection is a concave ellipse-like figure (or convex, maybe, depending on assumed perspective). Is this, then, the coin’s real apparent shape, to speak most accurately? Does the world look concave? I can almost (but only almost) warm up to the idea – it seems, actually, better to me than saying the world looks flat. The psychologist Steven Lehar, who considers the geometry of apparent size and shape more explicitly than most, does appear to conclude that there’s a sense in which flat surfaces look concave (2003, p. 399). However, holding a large, flat object a foot before my face tends to dispel my attraction to that view.
This flawed geometry is a serious, perhaps fatal difficulty for any view committed to the elliptical appearance of the tilted coin, even if ellipticality is only one aspect of the coin’s appearance. Nor is the difficulty new, even it is rarely noticed by philosophers. Leonardo da Vinci emphasizes the point in his unfinished treatise on painting; proportionality on a flat, painted surface is not the same, he says, as proportionality in appearance to the eye. A ball drawn at a height must be elongated to appear round; objects drawn in very near perspective will appear monstrously foreshortened on the painting surface unless that surface is viewed from an angle that also foreshortens the appearance of the painted surface in just the same way (1519/1989, p. 59-61). Perhaps, then, you might suggest, we are like Leonardo’s correctly situated viewer, and some mechanism compensates for the distortions in planar projection, so that the obliquely viewed sphere does not in fact look larger than the sphere directly ahead, despite its larger appearance in the plane? But then the geometry of visual appearance is no longer the geometry of the projective plane after all. What is it instead? The key question is only pushed back, not answered.
Could it be that there’s an ellipse upon the retina? Well first, of course, the retina is not flat, but curved, so the figure there is not an ellipse but a convex ellipsoid – a figure not even approximately flat if the object in view occupies a large visual angle. Just as importantly, we shouldn’t take it for granted that how things appear on the retina is how things look, phenomenologically. For starters, the retinal image is upside down, has a hole in it where the optic nerve enters, and is not actually one but two – one for each eye, slightly different.
There appears to be no plausible geometry of flattism, no means of transforming the outward circle into the inward ellipse that doesn’t, when generalized, lead to absurdities.
iv.
Is it just obvious and undeniable that the coin appears or looks (in some sense) elliptical, in a way that no geometrical cavils can touch? That seems to be the majority view, both among scholars and among the ordinary people I’ve quizzed on the topic. No elliptical appearance is obvious to me, but of course that’s just confessional, just me, and maybe I’m being obtuse or willfully blind. Quite possibly so!
However, I’ll tell you what I suspect. I suspect that our inclination to regard the apparent shape of the coin as an ellipse and the farther lightposts as smaller – our inclination to attribute to visual appearances or visual experience what I’ll henceforth call projective distortions – is due to overanalogizing visual experience to flat media such as paintings or snapshots. Noë himself suggests that theorists have often over-analogized visual experience to snapshots, mistakenly attributing to visual experience photographically rich detail from the center far into the periphery (more on this in Chapter 7). What I’m suggesting is that the mainstream community in philosophy of perception, including Noë, over-analogizes to pictures in a different way, taking visual experience or “apparent shape” to be, in some sense, flat like a picture: The coin “looks” elliptical because that’s how we’d paint it.
We over-analogize the mind quite often, I suspect, casting what’s difficult and recondite in terms of better-known outward media and technologies, then misattributing features of those technologies back into the mind. If you’re a connectionist (emphasizing the value of a certain sort of non-classical computation) or a fan of John Searle (1984), you might think many philosophers and cognitive psychologists in the 1970s and 1980s over-analogized thought to classical computation. (Earlier materialist philosophers analogized thought to clockwork or hydraulics.) I suggested in Chapter 1 that Americans in the 1950s similarly over-analogized dreams to movies, going so far as to erroneously claim that most dreams are black and white.
v.
I’m not sure how to establish what
I’ve just suggested. Maybe it can’t be
established. But here’s a conjecture
which, if true, may support the idea: Theorists writing in contexts where
vision isn’t typically analogized to two-dimensional projective media will be substantially less likely to attribute
projective distortions to visual experience – especially planar projective
distortions – than will theorists writing in cultural contexts where flat media
metaphors dominate. Two historical
periods are especially relevant to this hypothesis: ancient
If a signet is correctly applied, the impression on wax will accurately match, in complement, the entire shape of the signet, with a correspondence part-for-part that doesn’t vary with the circumstances of application. Unlike photographs or paintings, wax impressions don’t reflect different parts of their subject, or take on a different arrangement of shapes, with variations in perspective (though, of course, we may see a wax impression from different perspectives, or a signet may be engraved, incidentally, with a perspectivally represented scene). Now perhaps this absence of perspective is a weakness in the wax-signet analogy: Clearly perception – vision especially – is perspectival. Furthermore, vision is perspectival in a way resembling painting and photography in at least the following respect: A picture will portray (and omit) almost exactly the same parts of its subject a viewer would see (and not see) from that side. In this respect at least, the picture analogy is superior to the wax-signet analogy for vision. But of course it doesn’t follow from this alone that things look flat.
Aristotle famously employs the signet analogy for perception in De Anima (4th c. BCE/1936, 424a, 435a) and De Memoria (4th c. BCE/1906, 450a, though in the latter passage he also employs the picture analogy). He writes, for example, that “sense is that which is receptive of the form of sensible objects without the matter, just as the wax receives the impression of the signet ring without the iron or the gold” (424a). In neither of these works, nor in the related works I’ve reviewed, does Aristotle attribute projective distortions to visual appearances.[5] Epicurus embraces the signet analogy (see Letter to Herodotus circa 300 BCE/1926, 49 [note the word εναποσφραγίσαιτο, from to impress or imprint in or on] and the description of his view in Plutarch’s Brutus circa 100 CE/1918, XXXVII) and stresses that our impressions are the same shape as the objects perceived – that is, apparently, not projectively distorted.[6] Sextus Empiricus, though critical of the signet analogy in some places (e.g., Against the Logicians 2nd c. C.E./2005, I.228, 250-251, 372, II.400; Outlines of Skepticism 2nd c. CE/1994, II.70), appears to employ it uncritically in others (AL I.293; OS I.49) and never (that I can find) analogizes perception to having a picture in the mind. He’s a particularly telling case, I think, because he repeatedly emphasizes variation and distortion in sensory appearances, offering extensive catalogues at, e.g., OS I.44-52, 100-127; AL I.192-209, 414. For example, Sextus notes that things look different after one has stared at the sun, or when one presses the side of one’s eye; that mirrors can change the appearance of things; that oars look bent in water; that what appears in motion or at rest depends on whether one is on the ship or the shore; and so on. Sextus is the greatest of the Greek skeptics – or at least the one with the largest body of extant work – and his skeptical arguments require that he stress how sensory appearances vary with differences in situation; it’s one of his most famous and central points. And yet I can discover no unambiguous example of two-dimensional projective distortion. It’s difficult to imagine that Sextus would have left phenomena of this sort off his lists of perspectival variation had they occurred to him.
Before we consider two potentially ambiguous passages in Sextus, and also in Plato, I must emphasize the distinction between illusion and projective distortion. The two are very different: One can reject all varieties of flattism and yet hold that we may on some occasions see a round object as elliptical or a distant object as smaller than it is. In fact, the latter might be quite common: Young children systematically underestimate the size of distant objects. Adults’ judgments are more accurate, but whether that’s because we no longer suffer the illusion or whether, instead, it’s that we compensate for it in our judgments about objective size, is unclear (Gilinsky 1951; Epstein et al. 1961; Leibowitz et al. 1967; Higashiyama and Shimono 1994; Granrud 2009). If there is a persistent size illusion with distance, cognitively compensated for, that might explain my greater attraction to the shrinking streetlights than the elliptical coin: There would still be some truth in the thought that they look smaller – not because any sort of flattism is true but rather because the visual system tends to misjudge the size of distant objects. It wouldn’t follow that the coin looks elliptical or a rectangular table trapezoidal. But is there a persistent illusion of smallness in distant things? It’s interesting to me, actually, how hard it is to distinguish veridical perception from perception of known illusions adequately compensated for in judgment (for further thoughts see this note[7]). Regardless, however, everyone has to permit some illusion, no matter their take on projective distortion. In fact, it’s probably best to think of projective distortion as veridical rather than illusory: As Noë emphasizes, the coin’s elliptical appearance at an angle underwrites our knowledge of its objective circularity; the distant streetlight’s looking about half the height of the near one underwrites our knowledge that it is actually the same size, about twice as far away. Perspectival distortions are not, on this view, misleading illusions but accurate representations of perspectival properties from a particular point of view.
Although I can’t quite extricate myself from that tangle of issues, this much seems clear: Since everyone must allow for the existence of illusion, we cannot automatically assume that whenever an author says that something appears the wrong size or shape, he embraces the existence of perspectival distortion in the relevant sense. Sextus writes that a colonnade viewed from one end appears to narrow, but appears symmetrical when viewed from the middle,[8] and he writes that from a distance a square tower may look round or a large thing small (OS I.118). Someone who finds flattism a natural and obvious position might be tempted to see projective distortion in these claims, but I believe the examples are more naturally read as cases of illusion than projective distortion. If Sextus were speaking here of projective distortion, he should say that the colonnade narrows at both ends when viewed from the middle, rather than contrasting as he does the narrowing and the symmetricality. Illusions in the perception of columns were well known to the ancient Greeks, and famously employed in the design of the Parthenon; there’s no reason not to think this is what Sextus had in mind. Likewise, just as we can misperceive a square tower in the distance as round, Sextus seems to be saying, we can misjudge its size. No planar projection need be involved; he needn’t be accepting flattism. Epicurus makes a similar claim about distant towers, reported by Sextus in AL I.208-209 and presumably influencing Sextus’s own claim; and Epicurus explains both the roundness and the smallness, not by planar projection (how could something square in that way become round, anyhow?) but rather to the wearing off and smoothing of the edges of effused images from the distant tower in the course of their travel to the eye. (See also Euclid’s Optics circa 300 BCE/1945, fig. 9, for a related but slightly different explanation.)
Plato is another interesting case. His use of analogy is unusual in the ancient Greek context: Although he employs the wax signet analogy for memory (in the Theaetetus 4th c. BCE/1961, esp. 191c-194d) he does not appear to use it for perception; and he does in at least one place compare visual appearances and paintings (Republic 4th c. BCE/1961, X.597e-598c, where he says the painter imitates the appearance of the couch); so the ancient Greeks aren’t entirely univocal in their choice of analogies. Plato also, in the Protagoras, says that “the same magnitudes seem greater to the eye from near at hand than they do from a distance” (4th c. BCE/1961, 356c, p. 347); but this passing remark is too brief to determine if Plato has misperception or projective distortion in mind. In the Sophist (4th c. BCE/1961, 235e-236a) a “stranger” suggests that the tops of colossal statues look too small unless artists render them disproportionately large. But this can’t be a matter of projective distortion: If the artists were to try to compensate fully for projective distortion, that would require radical enlargement of the tops of a colossal statues; and of course there’s no need to compensate for ordinary projective distortion anyway, since a proportionate colossus should, in the relevant sense, “look smaller” at the top, if it is also to look objectively proportionate. Again, the remark appears to concern illusion, and the Greeks’ Parthenonesque tricks of design to please the eye.
In the ancient Greek literature that I’ve reviewed, I’ve found only a few explicit comparisons of visual perception, or even visual imagery, to sketches or paintings. And I’ve found no clear case of any ancient Greek attributing projective distortions to visual appearances. I’ve found a few remarks, discussed above, that might be interpreted either way – though it’s worth noting that even these pertain mainly to size distortion. No elliptical coins, no flat-looking globes.
Am I setting the
bar to high? What, one might wonder,
would count as an unambiguous attribution of perspectival distortion? Well, one needn’t look farther than ancient
In ancient Egypt, Euclid writes that “if the line falling from the eye to the center of the circle is not at right angles to the plane of the circle nor equal to the radius and does not enclose equal angles, the diameters with which it makes unequal angles will appear unequal” (Optics, figure 35). In other words, the obliquely viewed circle will appear to the eye to have the unequal diameters (longer, say, side-to-side than top-to-bottom) characteristic of an ellipse. Indeed, throughout the Optics, Euclid characterizes apparent size and shape in terms of visual angle (e.g., figure 5), not planar projection. His angular geometry, like the geometry of projection onto a sphere, does not imply the stretching of objects off the central line of sight (though I think it’s not straightforward how depth is experienced on Euclid’s view). Ptolemy, following Euclid in Egypt centuries later, espouses similar views in his own Optics (2nd c. CE/1996). These cases do not, I think, falsify my conjecture but rather confirm it: The ancient Italians and Egyptians seem much less enamored of the wax signet analogy. The ancient Egyptian Plotinus, for example, regularly vilifies the analogy in his Enneads (3rd c. CE/1966-1988, e.g., at III.6.2 and throughout IV.5-6). But neither does comparison to flat media seem to be common in these literatures. Fittingly, then, the perspectival distortions in Lucretius, Euclid, and Ptolemy do not show a planar character. Lucretius describes the apparent shape of his colonnade as a cone, and Euclid and Ptolemy use an angular geometry.[9]
(If you read English translations of the Greek classics with my hypothesis in mind you may notice many occurrences of the word “picture” in discussions of visual imagery – in discussions, that is, not of visual sensations but of visual imaginings. In most of the cases I’ve examined, it appears to be the translator bringing in the analogy; the original Greek texts do not explicitly suggest it. Such translations may arise because calling images “pictures” almost doesn’t seem metaphorical to contemporary English speakers. Is this because images actually are flat?)
vi.
The stereoscope, invented by Charles Wheatstone in the 1830s, and popular in 19th century parlors, served as the preferred analogy for binocular vision among some of the early introspective psychologists (e.g., Helmholtz 1856/1909/1962; Mach 1886/1959; Wundt 1896/1897; Titchener 1901-1905, 1910). A stereoscope holds two photographs, taken from slightly different perspectives, and presents one to each eye. If the perceiver succeeds in “fusing” the two pictures, she experiences a lively three-dimensional effect. Although stereoscopes are perspectival as signet impressions are not, the stereoscopic image is not a simple two-dimensional projection.
In accord with my conjecture in section iv, the psychologists favoring stereoscopy as an analogy for sight also tend to avoid saying (except in cases of outright illusion) that “apparent size” varies with distance or that the circle viewed obliquely “looks” elliptical – though Hermann von Helmholtz is a notable exception. Conversely, authors not as swept up in stereoscopy (e.g., Dewey 1886), or who seem generally to prefer the picture analogy (e.g., James 1890/1981), more frequently attribute projective distortions to experience. (Do the different analogies drive the different descriptions of experience, or vice versa?)
Psychologists analogizing vision to stereoscopy tend to stress the difference between monocular and binocular vision. Ernst Mach, for example, in presenting a sketch of what he takes to be a moment of his visual experience, emphasizes that a flat picture can only adequately represent monocular vision; “stereoscopic” vision, he says, can’t be represented by a single plane drawing (1886/1959, p. 18-19; Noë, though he reproduces the sketch, does not mention this aspect of Mach’s presentation). Would Mach, then, have been willing to say that a circle viewed at an angle looks like an ellipse monocularly but not binocularly? To contemporary sensibilities this may seem strange: It seems – to me at least – that monocular vision just isn’t that different from binocular vision (though Brian O’Shaughnessy [2003] and Oliver Sacks [2006] appear to disagree with me on this point).[10] Binocular disparity (as late 19th-century psychologists well knew) is only one among many depth cues. The world doesn’t go flat and then puff out as I open and close one eye, I think. But of course in stereoscopy, the difference between monocular and binocular views is essential.
vii.
Psychologists fond of the stereoscope analogy also seem readier than others to find doubling in visual experience, like the doubling, perhaps, of an unfused image in a stereoscope. Titchener writes, for example:
[T]he field of vision... shows a good deal of doubling: the tip of the cigar in your mouth splits into two, the edge of the open door wavers into two, the ropes of the swing, the telegraph pole, the stem of another, nearer tree, all are doubled. So long, that is, as the eyes are at rest, only certain objects in the field are seen single; the rest are seen double (1910, p. 309).
That most people fail to notice this, Titchener remarks, is “one of the curiosities of binocular vision”. Helmholtz writes similarly:
When a person’s attention is directed for the first time to the double images in binocular vision, he is usually greatly astonished to think that he had never noticed them before, especially when he reflects that the only objects he has ever seen single were those few that happened at the moment to be about as far from his eyes as the point of fixation. The great majority of objects, comprising all those that were farther or nearer than this point, were all seen double (1856/1909/1962, vol. 3, p. 6-7).
Now I must confess finding quite remarkable – almost unbelievable – the idea that most of what I see, most of the time, is doubled. However, P.L. Panum (1858) suggests that we shouldn’t be too surprised by people’s ignorance on this point. First, he says, double images are generally indefinite and foggy (unbestimmten and nebelhaften), partly because they usually arise from objects that are not at the focal distance to which the eyes are at that moment accommodated. And second, since the eyes generally converge upon whatever object we are attending to, through their convergence making it appear single, it is generally only unattended and thus quickly forgotten objects that appear double.[11]
Holding my finger about four inches before my nose and focusing my eyes in the distance, I find that the finger does in some sense look doubled. With a little more effort, if I focus on my finger a foot in front of my face, I can see objects in the distance as doubled. (It helps if the object is a small light source and the environment relatively dark; it also helps if I open and shut one eye first.) But is this how things seem most of the time? As I took my morning stroll today, I repeatedly considered this question. I held my finger a foot in front of my face and focused on it, considering how the houses in the distance looked, or the car parked on my left. (One neighbor seeing this smiled at me, embarrassed on my behalf for my strange behavior – such are the risks, I suppose, of science, or philosophy, or history, or whatever it is I’m doing in this book.) I can only say that I was struck by the singleness of everything, contra Titchener, Helmholtz, Panum, etc. This singleness was sometimes blurry; but blurriness is not much like doubling, except perhaps when both are very minor or when the target object is unadorned and amorphous.
It could be that I’m different from most people. I was diagnosed with amblyopia (“lazy eye”) as a child, and even now I have, I think, an unusually dominant left eye, so that I find it natural to close my right eye in bright sunlight and find it very difficult to freely fuse “Magic Eye” autostereograms. So maybe my visual experience depends less on binocular cues than is usual and consequently I differ from the majority in my experience of double images, visual depth, etc. When I presented the ideas of this section to my undergraduate seminar in 2007, I was surprised to find that all eight students reported seeing many of the things around them as double, and one student remarked that for years he had been aware of the pervasive doubling of things away from the point of focus. On the other hand, Stephen Palmer, in his influential textbook Vision Science, suggests that we don’t ordinarily experience binocular disparity as doubleness, but rather as depth, except when we specifically attend to that disparity (1999, p. 209; see also Lee and Dobbins 2006). The issue has not been systematically explored by contemporary psychologists.
It would be in keeping with the general theme of these last two chapters if I could link the rise and (partial) decline of the view that most objects are seen double with the rise and decline in the popularity of stereoscopes. And indeed there does seem to be some synchrony. Nevertheless, the view that experience is pervasively doubled antedates the invention of the stereoscope by a millenium and a half, tracing back at least to Ptolemy; so the media analogy is at best a partial explanation. Also operative here, I think, is the theory of the horopter – the horopter being a term (invented by François de Aguilón in 1613) for the region of space from which rays radiating to each eye will fall on corresponding parts of the retina, with the distance of that region depending on the degree of convergence of the eyes. (Ptolemy’s version of this theory, in Optics II.27-44, does not specifically invoke the retina. Other important pre-stereoscope advocates of pervasive doubling are Reid [1764/1997 VI.13]; Jan Purkinje [1819/2001, p. 102-104]; and Johannes Müller [1837-1840, vol. 2, p. 376-387]; a good recent discussion of the horopter – virtually silent on the issue of doubling – is Schreiber et al. 2008.) Unfortunately, I see no straightforward way to assess whether the geometrical beauty of the horopter theory, and perhaps the invention of the stereoscope, enabled the discovery of the pervasive doubling of visual experience, or whether they instead misled researchers into attributing doubling that is, at most, present only in unusual cases or when the fact of disparity is attended to.
Is the question really so difficult though? Shouldn’t the difference between a pervasively doubled and a pervasively singular visual field be so huge and obvious that – despite Panum’s cautions – it would be almost impossible for a careful observer to get it wrong? It would be tempting, perhaps, to attribute disagreements on the matter entirely to terminological differences, if only the terminology weren’t so seemingly straightforward. Who can’t, simply by putting her finger before her nose, grasp the relevant sense of “appearing double”? Do people, then, though outwardly similar, just visually experience the world in radically different ways?
viii.
Of course we can tell by looking that an obliquely viewed coin would project as an ellipse upon an intervening plane. But we can also tell that it would project as a circle onto the ceiling, project as two ellipses onto two planes at slightly different angles (one for each eye, say), project as a concave ellipsoid on the exterior of a sphere, and be prone to make a certain impression in wax. Surely the coin looks different from different perspectives, despite its objective constancy. (Similarly, perhaps, the shadowed part of a wall looks different from the sunlit part, even though we can tell by looking that it’s painted a single color; and a person sounds different far away than she does nearby even though we know by hearing that she is speaking no less loudly.) But whether the differences in the coin’s appearance as I move my head are well captured by saying it “looks elliptical” – that’s another question.
David Hume writes:
’Tis commonly allowed by philosophers, that all bodies, which discover themselves to the eye, appear as if painted on a plain surface (1740/1978, p. 56).
And G.E. Moore says, after holding up an envelope:
Those of you on that side of the room will have seen a rhomboidal figure, while those in front of me will have seen a figure more nearly rectangular (1953, p. 33).
I suppose it isn’t as obvious to me
as it has been to many others that there is any
sense in which such remarks are true.
But I’m not sure how to go about resolving this question. Staring longer at the penny leaves me only
more perplexed.