Do Things Look Flat?
Eric Schwitzgebel
Department of Philosophy
951 827 4288
eschwitz@ucr.edu
July 7, 2006
Do Things Look Flat?
Abstract
Does a penny viewed at an angle in
some sense look elliptical, as though projected on a two-dimensional
surface? Many philosophers have said
such things, from Malebranche (1674/1997) and Hume (1739/1978), through early
20th-century sense-data theorists, to Tye (2000) and Noë (2004). I confess that it doesn’t seem this way to
me, though I’m somewhat baffled by the phenomenology and pessimistic about our
ability to resolve the dispute. I raise
geometrical complaints against the view and conjecture that views of this sort
draw some of their appeal from over-analogizing visual experience to painting
or photography. Theorists writing in
contexts where vision is typically analogized to less-projective media – wax
signet impressions in ancient
Word count: Main text, including footnotes and references: 4339 words
Word count, abstract: 131 words
Plus one figure
Do Things Look Flat?
i.
I’ve put a penny on my desk, and I’m viewing it at an angle. Does it look circular? Or, instead, do I only know or judge that the penny is circular, while the figure it presents to my sight – its actual visual appearance – is an ellipse? I gaze out my window and see a row of streetlights. Does it look like they shrink as they recede into the distance? Or do they all look the same size? Get out a penny, open the blinds, try it yourself. (I’ll wait.) What do you think?
A long line of philosophers, stretching at least from Malebranche (1674/1997) through Ayer (1940), Chisholm (1957), and Austin (1962) to Tye (2000), Noë (2004), and Kelly (forthcoming) has said the following: There’s a sense in which the obliquely-viewed penny looks elliptical and the distant streetlights look smaller and a sense in which they don’t. Tye says that the coin looks like an object that really is round and also that the coin looks “elliptical from here”, that the streetlights look the same objective size but also that the nearer ones look “larger from here”. Noë, developing a similar view, asserts that it’s just what it is for a coin to look circular that it presents varying elliptical appearances depending on the angle from which it’s seen. Noë stresses that our visual experience always has, simultaneously, two “aspects” – a perspectival aspect (corresponding to the coin’s elliptical appearance) and an aspect reflecting our experience of the constancy of the objects we see (corresponding to our experience of the coin as genuinely circular, regardless of viewing angle). Kelly, criticizing Noë, argues that we don’t experience the circularity and ellipticality simultaneously but rather flip between the two ways of experiencing the coin, much as we flip between different ways of seeing an ambiguous figure (with circularity being the primary and ordinary experience). All agree with the apparently commonsensical view that the penny both looks circular (in one sense) and also has an elliptical “apparent shape” that we at least sometimes experience.
Now, can we really have it both ways like this? And if so, how exactly does that play out in experience – more as Noë suggests, or more as Kelly suggests, or neither way? Or is some purer just-the-circle or just-the-ellipse view right? What, exactly, do I visually experience as I look at the penny? That seems like a substantive, interesting question – a question, furthermore, of the sort many philosophers have thought we have excellent, perhaps infallible epistemic resources to answer – a question, that is, about the intrinsic properties of one’s own ongoing conscious experience. Why do I find such questions baffling?
For what it’s worth, as I stare at the penny now, I’m inclined to say it looks just plain circular, in a three-dimensional space – not elliptical at all, in any sense or by any effort I can muster. I can’t manage any Gestalt switch; I discern no elliptical “apparent shape”.
ii.
Now I don’t wish to be dogmatic about that last point. I feel uncertain in my own introspections. The streetlights in the distance do, maybe, look smaller, in a way. When I tilt the coin far enough, I start to feel the pull of the idea that it presents an elliptical appearance. Can I say these things consistently with denying the coin’s elliptical appearance at a 45˚ angle? Rotating the coin back from 80˚ to 45˚, does the impulse to say it appears in some sense elliptical at some point evaporate?
I confess I’m perplexed. Perhaps my phenomenology is disorganized, or not organized in a geometrically simple way? Or maybe my terms and concepts are muddled? What is it for something to “look elliptical”? Is the dispute, perhaps, entirely linguistic, or purely theoretical, while the phenomenology itself, considered on its own, is absolutely obvious?
Or am I simply a poor introspector? Maybe the fact that my own phenomenology in this case doesn’t seem obvious to me reveals introspective ineptitude on my part. I mean that remark not at all ironically or disingenuously. And yet I’m not sure I should trust other philosophers’ introspections either – even where they agree, even despite the broad consensus in contemporary philosophy about the elliptical “apparent shape” of the coin. Nor am I hopeful (as Kelly is, for example) that psychological experimentation will yield cleanly interpretable results in matters of this sort.
I wish I could find my way through this morass. I can’t. So I aim to drag you down into it with me.
iii.
There are several ways to transform a circle into an ellipse, but the most natural in this context seems to be to project it obliquely onto a two-dimensional plane – presumably a plane perpendicular to the line of sight. Let’s suppose that’s how the geometrical transformation is supposed to proceed in the case of the coin: The coin “looks elliptical” or has an “elliptical apparent shape” because projecting it along the line of sight onto a plane perpendicular to that line produces an elliptical figure. Plausible enough?
It’s tempting, then, to generalize: The apparent shape of any normal object is determined by its two-dimensional projection onto a plane perpendicular to the line of sight. This seems the most straightforward development of the view. None of the authors so far discussed, to my recollection, explicitly wards against this interpretation, and Tye comes very close to endorsing it explicitly.[1] But problems loom.
First, it would seem to follow that my hat, viewed from the top, also appears elliptical, that the orange in front of me appears circular, that the obliquely viewed book on my desk appears (roughly) hexagonal – and, in short, that everything looks or appears (in the relevant sense of “looks” or “appears”) two-dimensional, flat. Do we really want to be committed to this? The peculiarity of this view can be missed when the object in question, like a penny, is already something approximately flat.
I don’t know whether most of the philosophers who claim that the coin, in some sense, presents an elliptical “apparent shape” would accept the view that everything (in that same sense) looks flat; I suspect not. Yet it isn’t evident exactly where to put on the brakes. Can something’s apparent shape be defined by its two-dimensional projection without its presenting any sort of flat appearance? Well maybe; but that seems a rather uncomfortable sort of view.
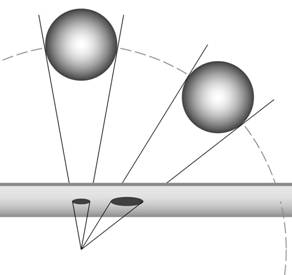
Planar projection also invites the question of how to account for the streetlights smalling off into the distance. We can render the farther ones smaller on the plane by projecting along lines that converge at the eye – no problem there; that seems natural enough. But a peculiar result follows from the fact that lines coming from the side will intersect the plane obliquely: The planar projections of objects off the central line of sight will be considerably larger than their straight-ahead counterparts – weirdly larger, if projective size is supposed to be isomorphic to apparent size (see fig. 1).
-----------------------------------
Insert fig. 1 about here
-----------------------------------
Note the considerably larger shadow the right figure casts in the plane. The rays crossing the plane obliquely spread over a larger area. (For the same reason, winter is colder than summer.)
A natural way to avoid this result would be to project objects not onto a plane but rather onto a sphere centered at the eye. (Imagine bending the plane on the right side back until it forms a sphere centered around the point of convergence.) Using spherical rather than planar projection would also capture the idea that apparent size varies with visual angle subtended. But now we’ve lost our ellipse. The projection of a circular region onto a spherical surface isn’t elliptical: The ellipse is a planar figure. The resulting projection is a concave ellipse-like figure (or convex, if the projection passes through the interior of the sphere). Is this, then, the coin’s real apparent shape, to speak most accurately? Does the world look concave? I can almost (but only almost) warm up to the idea – it seems, actually, better to me than saying the world looks flat.[2]
iv.
Is it just obvious and undeniable that the coin appears or looks (in some sense) elliptical, in a way that no geometrical cavils can touch? It’s not obvious to me. But of course that’s just confessional, just me, and maybe I’m being obtuse or willfully blind. Quite possibly so!
However, I’ll tell you what I suspect. I suspect that our inclination to regard the apparent shape of the coin as an ellipse and the farther lightposts as smaller – our inclination to attribute to visual appearances or visual experience what I’ll henceforth call projective distortions – is due to over-analogizing visual experience to flat media such as paintings or snapshots. Noë himself interestingly suggests that theorists have often over-analogized visual experience to snapshots, mistakenly attributing to visual experience photographically rich detail from the center far into the periphery. What I’m suggesting is that the mainstream community in philosophy of perception, including Noë, over-analogizes to pictures in a different way, taking visual experience or “apparent shape” to be, in some sense, flat like a picture: The coin “looks” elliptical because that’s how we’d paint it.
We over-analogize the mind quite often, I suspect, casting what’s difficult and recondite in terms of better-known outward media and technologies, then misattributing features of those technologies back into the mind. If you’re a Searle fan or a connectionist, you might think we did that in the 1970s and 1980s, analogizing thought to classical computation. (Earlier philosophers analogized thought to clockwork or hydraulics.) My favorite example of over-analogizing, though, is the over-analogizing of dreams to movies. This went so far that in the 1950s the overwhelming majority of North Americans said they dreamed in black and white! (Now we say we dream in color. I’m not sure that’s true either. See Schwitzgebel 2002; Schwitzgebel, Huang, and Zhou 2006.)
v.
I’m not sure how to establish what
I’ve just suggested. Maybe it can’t be
established. But here’s a conjecture
which, if true, may support the idea: Theorists writing in contexts where
vision isn’t typically analogized to two-dimensional, projective media will be substantially
less likely to attribute projective distortions to visual experience than
those analogizing vision to painting or photography. Two historical periods are especially
relevant to this hypothesis: ancient
If a signet is correctly applied, the impression in the wax will accurately match, in complement, the entire shape of the signet, with a correspondence part-for-part that doesn’t vary with the circumstances of application. Unlike photographs or paintings, wax impressions don’t reflect different parts of their subject, or take on a different arrangement of shapes, with variations in perspective (though, of course, we may see a wax impression from different perspectives, or a signet may be engraved, incidentally, with a perspectivally represented scene). Now perhaps this absence of perspective is a weakness in the wax-signet analogy: Clearly, in some sense, perception – vision especially – is perspectival. Furthermore, vision is perspectival in a way resembling painting and photography in at least the following respect: A picture will portray (and omit) almost exactly the same parts of its subject a viewer would see (and not see) from that side. In this respect, at least, the picture analogy is superior to the wax-signet analogy for vision. But of course it doesn’t follow from this alone that the apparent shapes of things are projectively distorted.
Aristotle and Plato famously employ the signet analogy for perception and memory in De Anima (424a; 435a; see also De Memoria 450a where Aristotle employs both the signet and the picture analogy) and the Theaetetus (esp. 191c-194d), respectively. And indeed in these works, and in related works I’ve reviewed, neither ever attributes projective distortions to visual appearances, though they do discuss various puzzles about perception, and Plato provides other examples of variation in sensory appearance and judgment.[3] Epicurus embraces the signet analogy (see Letter to Herodotus 49 [note the word εναποσφραγίσαιτο] and Plutarch’s Brutus) and positively asserts that our impressions are the same shape as the objects perceived – that is, apparently, not projective distortions.
Sextus
Empiricus, though critical of the signet analogy in some places (e.g., Against
the Logicians I.228, 250-251, 372, II.400; Outlines of Skepticism
II.70), appears to employ it uncritically in others (
I’m no classical
scholar, but in the ancient Greek literature I’ve managed to review thus far,
I’ve found few explicit comparisons of visual perception, or even visual
imagery, to pictures or paintings. And
I’ve found no clear case of any ancient Greek philosopher attributing
projective distortions to visual appearances.
One does begin to see projective distortion, however, and perhaps a
decline of the wax analogy, with even as small a cultural shift as to ancient
(Translations of ancient Greek classics do often employ the word “picture” in discussions of visual imagery – that is, not visual sensations, but visual imaginings. In cases I’ve examined, it is usually the translator bringing in the analogy; the original Greek texts do not explicitly suggest it. Such interpretations may arise because calling images “pictures” almost doesn’t seem metaphorical to us. We’re even more prone to compare visual imagery to flat media than visual sensation. Is this because images are actually flat? Or does their seeming insubstantiality discourage comparison to more robust media regardless of their two-dimensionality or lack of it?)
vi.
Stereoscopes, which enjoyed a vogue in late 19th century parlors, served as the preferred analogy for binocular vision among some of the early introspective psychologists (e.g., Helmholtz 1867/1925; Mach 1886/1959; Wundt 1897/1897; Titchener 1901-1905, 1910). A stereoscope holds two photographs, taken from slightly different perspectives, and presents one to each eye. If the perceiver succeeds in “fusing” the two pictures, she experiences a lively three-dimensional effect. Although stereoscopes are perspectival as signet impressions are not, the stereoscopic image is not a simple two-dimensional projection.
In accord with the conjecture above, the psychologists favoring stereoscopy as an analogy for sight also tend to avoid saying (except in cases of outright illusion) that “apparent size” varies with distance or that the circle viewed obliquely “looks” elliptical – though Helmholtz is a notable exception. Conversely, authors not as swept up in stereoscopy (e.g., Dewey 1886), or who seem generally to prefer the picture analogy (e.g., James 1890/1981), more frequently attribute projective distortions to experience.
Psychologists analogizing vision to stereoscopy tend to stress the difference between monocular and binocular vision. Mach, for example, in presenting a sketch of what he takes to be a moment of his visual experience, emphasizes that a flat picture can only adequately represent monocular vision; “stereoscopic” vision, he says, can’t be represented by a single plane drawing (1886/1959, p. 18-19).[6] Would he, then, have been willing to say that a circle viewed at an angle looks like an ellipse monocularly but not binocularly? To contemporary sensibilities this may seem strange: It seems – to me at least – that monocular vision just isn’t that different from binocular vision (though see O’Shaughnessy 2003). Binocular disparity (as late 19th-century psychologists well knew) is only one among many depth cues. The world doesn’t go flat and then puff out as I open and close one eye, I think. But of course in stereoscopy, the difference between monocular and binocular views is essential.
Psychologists fond of the stereoscope analogy also seem readier than others to find doubling in visual experience, like the doubling, perhaps, of an unfused image in a stereoscope. Titchener writes, for example:
[T]he field of vision … shows a good deal of doubling: the tip of the cigar in your mouth splits into two, the edge of the open door wavers into two, the ropes of the swing, the telegraph pole, the stem of another, nearer tree, all are doubled. So long, that is, as the eyes are at rest, only certain objects in the field are seen single; the rest are seen double (1910, p. 309).
That most people fail to notice this, Titchener remarks, is “one of the curiosities of binocular vision”.[7], [8]
vii.
Of course we can tell by looking that an obliquely viewed coin would project as an ellipse upon an intervening plane. But we can also tell that it would project as a circle onto the ceiling, project as two ellipses onto two planes at slightly different angles (one for each eye, say), project as a concave ellipsoid on the exterior of a sphere, and be prone to make a certain impression in wax. Why should one rather than another of these facts, or none of them, be regarded as determining the “appearance” of the coin? Is there really something in our experience that settles this?
Hume writes:
‘Tis commonly allowed by philosophers, that all bodies, which discover themselves to the eye, appear as if painted on a plain surface (1739/1978, p. 56).
And G.E. Moore says, after holding up an envelope:
Those of you on that side of room will have seen a rhomboidal figure, while those in front of me will have seen a figure more nearly rectangular (1953, p. 33).
I suppose it isn’t as obvious to me as it has been to many others that there is any sense in which such remarks are true. But I’m not sure how to go about resolving this question. Staring longer at the penny leaves me only more perplexed.[9]
Austin,
John (1962). Sense and sensibilia.
Ayer,
Alfred J. (1940). Foundations of
empirical knowledge.
Bowen,
Alan C. and Robert B. Todd (trans., 2004).
Cleomedes’ Lectures on Astronomy.
Chisholm,
Roderick M. (1957). Perceiving.
De
Lacy, Phillip H. and Estelle A. De Lacy (ed. and trans., 1978). Philodemus: On Methods of Inference. Bibiopolis:
Dewey,
John (1886). Psychology.
Helmholtz,
Hermann (1867/1925). Treatise on
physiological optics. Ed. J.P.C.
Southall.
Hume,
David (1739/1978). A treatise of
human nature. Ed. L.A. Selby-Bigge
& P.H. Nidditch.
Irwin,
Terence, and Gail Fine (ed. and trans., 1995).
Aristotle: Selections.
James,
William (1890/1981). Principles of
psychology.
Kelly,
Sean (forthcoming). Content and
constancy. Philosophy &
Phenomenological Research.
Lehar, S. (2003). Gestalt isomorphism and the primacy of subjective conscious experience: A Gestalt Bubble model. Behavioral and Brain Sciences 26, 375-444.
Locke,
John (1690/1975). An essay concerning
human understanding. Ed. P.H.
Nidditch.
Mach,
Ernst (1886/1959). The analysis of
sensations. Trans. C.M.
Williams.
Malebranche,
Nicolas (1674/1997). The search after
truth. Trans. T.M. Lennon.
Moore,
George Edward (1953). Some main
problems of philosophy.
Noë,
Alva (2004). Action in perception.
O’Shaughnessy,
Brian (2003). Consciousness and the
world, new ed.
Price,
H. H. (1932). Perception.
Reid,
Thomas (1764/1997). An inquiry into
the human mind. Ed. D.R.
Brookes.
Schwitzgebel, Eric (2002). Why did we think we dreamed in black and white? Studies in History and Philosophy of Science 33, 649-660.
Schwitzgebel, Eric (in preparation). The unreliability of naive introspection.
Schwitzgebel, Eric, Huang, C., and Zhou, Y. (2006). Do we dream in color? Cultural variations and skepticism. Dreaming 16, 36-42.
Smith,
J.A. (trans., 1931). De Anima. In The Works of Aristotle. Ed. W.D. Ross.
Titchener,
E.B. (1901-1905). Experimental
psychology.
Titchener,
E.B. (1910). A text-book of
psychology.
Tye,
Michael (2000). Consciousness, color,
and content.
Wang
Yangming (early 16th c./1963).
Instructions for practical living and other Neo-Confucian writings. Trans. W.-t. Chan.
Wundt, Wilhelm (1897/1897). Outlines
of psychology. Trans. C.H.
Judd.
Xunzi (3rd c. BCE/1964).
Hsün Tzu: Basic Writings.
Trans. B. Watson.
Xunzi (3rd c. BCE/1999). Xunzi. Trans. J. Knoblock and Z. Jue. Hunan People’s Publishing House.
Zhuangzi (4th c. BCE/1968).
The complete works of Chuang Tzu.
Trans. B. Watson.
Figure 1
[See accompanying JPEG file for a larger version of this figure.]