12. Network positions and social roles: The idea of equivalence
We have been examining some of the ways that structural analysts look at network data. We began by looking for patterns in the overall structure (e.g. connectedness, density, etc.) and the embeddedness of each actor (e.g. geodesic distances, centrality). Next, we introduced a second major way of going about examining network data by looking for "sub-structures," or groupings of actors that are closer to one another than they are to other groupings. For example, we looked at the meaning of "cliques" "blocks" and "bridges" as ways of thinking about and describing how the actors in a network may be divided into sub-groups on the basis of their patterns of relations with one another.
All of this, while sometimes a bit technical, is pretty easy to grasp conceptually. The central node of a "star" network is "closer" to all other members than any other member -- a simple (if very important) idea that we can grasp. A clique as a "maximal complete sub graph" sounds tough, but, again, is easy to grasp. It is simply the biggest collection of folks who all have connections with everyone else in the group. Again, the idea is not difficult to grasp, because it is really quite concrete: we can see and feel cliques.
Now we are going to turn our attention to somewhat more abstract ways of making sense of the patterns of relations among social actors: the analysis of "equivalence classes." Being able to define, theorize about, and analyze data in terms of equivalence is important because we want to be able to make generalizations about social behavior and social structure. That is, we want to be able to state principles that hold for all groups, all organizations, all societies, etc. To do this, we must think about actors not as individual unique persons (which they are), but as examples of categories -- sets of actors who are, in some defined way, "equivalent." As an empirical task, we need to be able to group together actors who are the most similar, and to describe what makes them similar; and, to describe what makes them different, as a category, from members of other categories.
Sociological thinking uses abstract categories routinely. "Working class, middle class, upper class" are one such set of categories that describe social positions. "Men and Women" are really labels for categories of persons who are more similar within category than between category -- at least for the purposes of understanding and predicting some aspects of their social behavior. When categories like these are used as parts of sociological theories, they are being used to describe the "social roles" or "social positions" typical of members of the category.
Many of the category systems used by sociologists are based on "attributes" of individual actors that are in common across actors. If I state that "European-American males, ages 45-64 are likely to have relatively high incomes" I am talking about a group of people who are demographically similar -- they share certain attributes (maleness, European ancestry, biological age, and income). Structural analysis is not particularly concerned with systems of categories (i.e. variables), that are based on descriptions of similarity of individual attributes (some radical structural analysts would even argue that such categories are not really "sociological" at all). Structural analysts seek to define categories and variables in terms of similarities of the patterns of relations among actors, rather than attributes of actors. That is, the definition of a category, or a "social role" or "social position" depends upon its relationship to another category. Social roles and positions, structural analysts argue, are inherently "relational." That's pretty abstract in itself. Some examples can make the point.
What is the social role "husband?" One useful way to think about it is as a set of patterned interactions with a member or members of some other social categories: "wife" and "child" (and probably others). Each one of these categories (i.e. husband, wife, child) can only be defined by regularities in the patterns of relationships with members of other categories (there are a number of types of relations here -- monetary, emotional, ritual, sexual, etc.). That is, family and kinship roles are inherently relational. The network analyst translates this idea by saying that there are "equivalence classes" of husband, wife, child, etc.
What is a "worker?" We could mean a person who does labor (an attribute, actually one shared by all humans). A more sociologically interesting definition was given by Marx as a person who sells control of their labor power to a capitalist. Note that the meaning of "worker" depends upon a capitalist -- and vice versa. It is the relation (in this case, as Marx would say, a relation of exploitation) between occupants of the two role that defines the meaning of the roles.
The point is: to the structural analyst, the building blocks of social structure are "social roles" or "social positions." These social roles or positions are defined by regularities in the patterns of relations among actors, not attributes of the actors themselves. We identify and study social roles and positions by studying relations among actors, not by studying attributes of individual actors. Even things that appear to be "attributes of individuals" such as race, religion, and age can be thought of as short-hand labels for patterns of relations. For example, "white" as a social category is really a short-hand way of referring to persons who typically have a common form of relationships with members of another category -- "non-whites." Things that might at first appear to be attributes of individuals are really just ways of saying that an individual falls in a category that has certain patterns of characteristic relationships with members of other categories.
Because "positions" or "roles" or "social categories" are defined by "relations" among actors, we can identify and empirically define social positions using network data. In an intuitive way, we would say that two actors have the same "position" or "role" to the extent that their pattern of relationships with other actors is the same. But, there are a couple things about this intuitive definition that are troublesome.
First, what relations to we take into account, among whom, in seeking to identify which actors are similar and which are not? The relations that I have with the university (as "Professor") are similar in some ways to the relations that my students have with the university: we are both governed by many of the same rules, practices, and procedures. The relations I have with the university are very different from those of my students in some ways (e.g. the university pays me, students pay the university). Which relations should count and which ones not, in trying to describe the roles of "professor" and "student?" Indeed, why am I examining relations among my students, me, and the university, instead of including, say, members of the state legislature? There is no simple answer about what the "right relations" are to examine; and, there is no simple answer about who the relevant set of "actors" are. It all depends upon the purposes of our investigation, the theoretical perspective we are using, and the populations to which we would like to be able to generalize our findings. Social network data analytic methods are of little use in answering these conceptual questions.
The second problem with our intuitive definition of a "role" or "position" is this: assuming that I have a set of actors and a set of relations that make sense for studying a particular question, what do I mean that actors who share the same position are similar in their pattern of relationships or ties? The idea of "similarity" has to be rather precisely defined. Again, there is no single and clear "right" answer for all purposes of investigation. But, there are rigorous ways of thinking about what it means to be "similar" and there are rigorous ways of actually examining data to define social roles and social positions empirically. These are the issues where there are some ways in which widely used methods can provide guidance.
What do we mean when we say that two actors have "similar" patterns of relations, and hence are both members of the same role or social position? Network analysis most broadly defines two nodes (or other more elaborate structures) as similar if they fall in the same "equivalence class." Frankly, that's no immediate help. But it does say that there is something that would cause us to say two actors (or other structures) are members of a "class" that is different from other "classes."
Now it becomes a question of what features of an actor's position place them into a "class" with other actors? In what way are they "equivalent?"
There are many ways in which actors could be defined as "equivalent" based on their relations with others. For example, we could create two "equivalence classes" of actors with out-degree of zero, and actors with out-degree of more than zero. Indeed, a very large number of the algorithms we've examined group sets of actors into categories based on some commonality in their positions in graphs.
Three particular definitions of "equivalence" have been particularly useful in applying graph theory to the understanding of "social roles" and "structural positions." We will look at these in the next three chapters on "structural equivalence," "automorphic equivalence," and "regular equivalence." Of these, "automorphic" has rarely been used in substantive work.
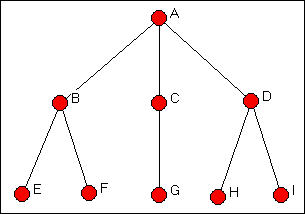
The basic ideas of these three kinds of equivalence are easily illustrated with a simple graph (developed by Wasserman and Faust). Consider figure 12.1, a simple graph of the relations among nine actors "A" to "I".
Figure 12.1 Wasserman-Faust network to illustrate equivalence classes

This graph provides particularly clear examples of how structural, automorphic, and regular equivalence differ. Let's look in more detail at these ideas, starting with the most restrictive notion of what it means for actors to be equivalent.
table of contentsTwo nodes are said to be exactly structurally equivalent if they have the same relationships to all other nodes. Structural equivalence is easy to grasp (though it can be operationalized in a number of ways) because it is very specific: two actors must be exactly substitutable in order to be structurally equivalent.
In figure 12.1 there are seven "structural equivalence classes." Can you find them?
Actors that are structurally equivalent are in identical "positions" in the structure of the diagram. Whatever opportunities and constraints operate on one member of a class are also present for the others. The nodes in a structural equivalence class are, in a sense, in the same position with regard to all other actors.
Because exact structural equivalence is likely to be rare (particularly in large networks), we often are interested in examining the degree of structural equivalence, rather than the simple presence or absence of exact equivalence.
Structural equivalence is the "strongest" form of that network analysts usually consider. If we soften the requirements just a bit, we can often find some interesting other patterns of equivalence.
table of contentsThe idea of structural equivalence is powerful because it identifies actors that have the same position, or who are completely substitutable. But, even intuitively, you can probably imagine other "less strict" definitions of what it means for two actors to be similar or equivalent.
Suppose that the graph in figure 12.1 described a franchise group of hamburger restaurants. Actor A is the central headquarters, actors B, C, and D are the managers of three different stores. Actors E and F are workers at one store; G is the lone worker at a second store; H and I are workers at the third store.
Even though actor B and actor D are not structurally equivalent (they do have the same boss, but not the same workers), they do seem to be "equivalent" in a different sense. Both manager B and D report to a boss (in this case, the same boss), and each has exactly two workers. These are different people, but the two managers seem somehow equivalent. If we swapped them, and also swapped the four workers, all of the distances among all the actors in the graph would be exactly identical. In fact, actors B and D form an "automorphic" equivalence class.
In diagram 12.1, there are actually five automorphic equivalence classes: {A}, {B, D}, {C}, {E, F, H, I}, and {G}. These classes are groupings who's members would remain at the same distance from all other actors if they were swapped, and, members of other classes were also swapped.
The idea of automorphic equivalence is that sets of actors can be equivalent by being embedded in local structures that have the same patterns of ties -- "parallel" structures. Large scale populations of social actors (perhaps like hamburger restaurant chains) can display a great deal of this sort of "structural replication." The faces are different, but the structures are identical.
Note that the less strict definition of "equivalence" has reduced the number of classes. If we are willing to go one important step further, we can reduce the complexity still further.
table of contentsTwo nodes are said to be regularly equivalent if they have the same profile of ties with members of other sets of actors that are also regularly equivalent. This is a complicated way of saying something that we recognize intuitively.
Two mothers, for example, are "equivalent" because each has a certain pattern of ties with a husband, children, and in-laws (for one example -- but one that is very culturally relative). The two mothers do not have ties to the same husband (usually) or the same children or in-laws. That is, they are not "structurally equivalent." Because different mothers may have different numbers of husbands, children, and in-laws, they will not be automorphically equivalent. But they are similar because they have the same relationships with some member or members of another set of actors (who are themselves regarded as equivalent because of the similarity of their ties to a member of the set "mother").
This is an obvious notion, but a critical one. Regular equivalence sets describe the "social roles" that are the basic building blocks of all social institutions. Actors that are regularly equivalent do not necessarily fall in the same network positions or locations with respect to other individual actors; rather, they have the same kinds of relationships with some members of other sets of actors.
In figure 12.1 there are three regular equivalence classes. The first is actor A; the second is composed of the three actors B, C, and D; the third is composed of the remaining five actors E, F, G, H, and I.
The easiest class to see is the five actors across the bottom of the diagram (E, F, G, H, and I). These actors are regularly equivalent to one another because a) they have no tie with any actor in the first class (that is, with actor A) and b) each has a tie with an actor in the second class (either B or C or D). Each of the five actors, then, has an identical pattern of ties with actors in the other classes.
Actors B, C, and D form a class because a) they each have a tie with a member of the first class (that is, with actor A) and b) they each have a tie with a member of the third class. B and D actually have ties with two members of the third class, whereas actor C has a tie to only one member of the third class; this doesn't matter, as there is a tie to some member of the third class.
Actor A is in a class by itself, defined by a) a tie to at least one member of class two and b) no tie to any member of class three.
As with structural and automorphic equivalence, exact regular equivalence may be rare in a large population with many equivalence classes. Approximate regular equivalence can be very meaningful though, because it gets at the notion of which actors fall in which social roles, and how social roles (not role occupants) relate to one another.
The three types of equivalence (structural, automorphic, and regular) have progressively less strict definitions of what it means for two actors to be "equivalent." And, as we make the definitions less strict (which is not the same as making them less precise!), we are able to understand social networks at increasing levels of abstraction.
Structural equivalence is the most "concrete" form of equivalence. Two actors are exactly structurally equivalent if they have exactly the same ties to exactly the same other individual actors. Pure structural equivalence can be quite rare in social relations, but approximations to it may not be so rare. In studying a single population, two actors who are approximately structurally equivalent are facing pretty much the same sets of constraints and opportunities. Commonly we would say that two actors who are approximately structural equivalent are in approximately the same position in a structure.
Automorphic equivalence is a bit more relaxed. Two actors may not be tied to the same others, but if they are embedded in the same way in the larger structure, they are equivalent. With automorphic equivalence, we are searching for classes of actors who are at the same distance from other sets of actors -- that is, we are trying to find parallel or substitutable sub-structures (rather than substitutable individuals).
Regular equivalence deserves special attention because it gets at the idea of the "role" that an actor plays with respect to occupants of other "roles" in a structure. The idea of a social role, which is "institutionalized" by normative and sanctioned relationships to other roles is at the very core of the entire sociological perspective.
The definitions of the forms of equivalence discussed here are quite precise (though my discussion doesn't have much mathematical rigor). The notions of equivalence provide quite rigorous ways of defining and thinking about core analytical tools in sociology -- individual's positions in groups, types of structures, and social roles. This is a huge advance over the sometimes quite imprecise and contradictory verbal treatments found in much of our literature.
But, real world social networks are often quite messy, may not be fully realized (that is, not in equilibrium), and/or may be badly measured. The search for equivalence in real data can be a somewhat complicated matter with a number of vexing choices to be made. We'll spend some time with these practical issues in the next three chapters.
1. How are network roles and social roles different from network "sub-structures" as ways of describing social networks?
2. Explain the differences among structural, automorphic, and regular equivalence.
3. Actors who are structurally equivalent have the same patterns of ties to the same other actors. How do correlation, distance, and match measures index this kind of equivalence or similarity?
4. If the adjacency matrix for a network can be blocked into perfect sets of structurally equivalent actors, all blocks will be filled with zeros or with ones. Why is this?
5. If two actors have identical geodesic distances to all other actors, they are (probably) automorphically equivalent. Why does having identical distances to all other actors make actors "substitutable" but not necessarily structurally equivalent?
6. Regularly equivalent actors have the same pattern of ties to the same kinds of other actors -- but not necessarily the same distances to all other actors, or ties to the same other actors. Why is this kind of equivalence particularly important in sociological analysis?
Application questions
1. Think of the readings from the first part of the course. Did any studies used the idea of structural equivalence or network role? Did any studies use the idea of regular equivalence or social role?
2. Think about the star network. How many sets of structurally equivalent actors are there? What are the sets of automophically equivalent actors? Regularly equivalent actors? What about the circle network?
3. Examine the line network carefully -- this one's a little more tricky. Describe the structural equivalence and regular equivalence sets in a line network.
4. Consider our classical hierarchical bureaucracy, defined by a network of directed ties of "order giving" from the top to the bottom. Make an adjacency matrix for a simple bureaucracy like this. Block the matrix according to the regular equivalence sets; block the matrix according to structural equivalence sets. How (and why) do these blockings differ? How do the permuted matrices differ?
5. Think about some social role (e.g. "mother") what would you say are the kinds of ties with what other social roles that could be used to identify which persons in a population were "mothers" and which were not? Note the relational character of social roles -- one social role can only be defined with respect to others. Provide some examples of social roles from an area of interest to you.